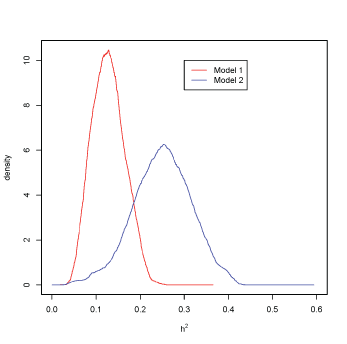
Figure 1: Heritability density with model 1, red, and model 2, blue.


Martínez-Ávila JC1* Guillén-Ponce C2 Earl J2 García-Cortés LA3
1Health Research Institute “Hospital 12 de Octubre”SCReN, CIBERESP, Spain*Corresponding author: Jose Carlos Martinez Avila, Health Research Institute “Hospital 12 de Octubre”SCReN (Spanish Clinical Research Network) CIBERESP (Biomedical Research Centre Network for Epidemiology and Public Health), Avda de Cordoba s/n, Edifico de actividades ambulatorias 6D, Madrid, Spain, E-mail: Jcmartineza.imas12@h12o.es
It is not straightforward to assess an individual genetic cancer risk in order to provide accurate and effective genetic counseling and secondary screening.
We present an analysis of the Minnesota Breast Cancer data based on the Best Linear Unbiased Prediction (BLUP) methodology to estimate an individual’s predicted genetic risk of developing cancer during their lifetime. The model uses cancer status, year of birth (yob), sex, age at last follow-up (endage) and number of births (parity) to estimate variance components in order to define hereditability. This tool that can also be applied to determine whether aggregation of cancer within a family is indeed due to hereditability or due to shared environmental factors. We provide an example of how this model can be used in the context of breast cancer but it can be applied to many cancer types with a genetic component.
We have obtained a reliable estimation of heritability for cancer (breast and prostate) between 0.1-0.2, different from zero, and meaningful additive values of cancer in the Minnesota Breast data set for each individual. BLUP is able to incorporate clinical and pathological information in the estimations and consider a polygenic inheritance model instead of an autosomal dominant model.
BLUP provides an additional tool for use in hereditary cancer and estimates the extent of heritability of cancer, calculating an individual genetic risk of cancer in family members and an approximation of the genetic risk of future descendants. In addition this tool can be used to assess the genetic basis of hereditary cancer in these families, either due to high risk alleles for low-medium risk alleles.
Best linear unbiased prediction; Additive genetic effect; Minnesota breast cancer-heritability; Genetic risk; Cancer risk assessment; Predictive models of cancer risk; Expected genetic values
BLUP: Best Linear Unbiased Prediction; ROH: Runs of Homozygosity; HPDI: High Posterior Density Interval; EGV: Expected Genetic Value; ROC: Receiver Operating Characteristic; AUC: Area under the ROC Curve.
Approximately 5-10% of all cancers have a hereditary component [1] and 9.4% of breast cancer cases have an affected first degree relative [2]. The presence of a pathogenic germline mutation in a known cancer gene means that this individual has a greater probability of developing a particular cancer type(s) during their lifetime. However, there is undoubtedly a large difference in cancer susceptibility depending upon the inheritance of different genetic variants and how these variants interact and in the genomic era we are discovering more genes and gene variants that are involved in complex diseases such cancer [3,4]. High risk genes are present at a low frequency in the general population while medium-lower risk genes appear at a higher frequency. In the absence of a known pathogenic germline mutation it is difficult to assess cancer risk especially when subjects harbor variants of unknown significance in these genes. There are still many medium-low risk alleles occurring at a high frequency that are still unknown as well as their effect to modify the development of cancer and there is an ongoing effort to decipher their contribution to cancer risk [5]. On the other hand in order to discover “soloist” genes we need to know how much of the phenotypic variation that we see is due to genetics.
A cancer is usually considered as sporadic cancer unless the patient has characteristics associated with familial cancer such as additional cancer cases within the family, an unusually early age at diagnosis, multiple tumors in the same individual such as bilateral tumors or different but related tumors such as breast and ovarian cancer. Guidelines for genetic and high risk assessment in these types of families include the National Cancer Comprehensive Network and NICE [6,7] among others.
In the particular case of breast cancer, around 25-30% of heritability can be attributed to mutations in the high to moderate risk genes (BRCA1, BRCA2, CHEK2, ATM, PALB2, PALB1, BRIP1, TP53, PTEN, CDH1 and STK11) [5,8]. The majority of these genes are involved in DNA repair and the regulation of cell-cycle checkpoints in response to DNA damage. Other low-moderate risk genes include BARD1, RAD51C and RAD51D [9-11]. Disease susceptibility in non-mutation carriers could be explained by a polygenic model where many susceptibility genes and polymorphisms within these genes combine to increase risk and produce the observed cancer phenotype [12]. Recent efforts in breast cancer research aim to discover the effect of rare alleles via high density next generation sequencing and coordinating international research groups into consortia [13].
Despite the fact that high quality pedigree information in humans is rare, mainly due to small family size, lack of clinical records or noninformative pedigrees, when it is recorded, a new opportunity arises to learn more about the genetic basis of cancer. The statistical definition of heritability is defined as the proportion of phenotypic variance attributable to genetic variance. When the variation explained by genetics is small, there is a need for accurate statistical methods to find individual genes.
In order to estimate an individual lifetime risk of developing breast cancer, family history and personal information have been combined in several statistical models under different assumptions. The Claus model focuses on Caucasians with an unknown germline mutation and information of first or second degree female relatives with breast cancer [14]. The Gail model is based on a multivariate logistic regression model in order to estimate breast cancer risk [15-17]. In this case the Gail model includes only information of the first-degree relatives and gives more importance to affected individuals. This feature of the Gail model may underestimate breast cancer risk in case of large family history of breast [18,19].
The likelihood that a BRCA1 or BRCA2 mutation is present is calculated using different approaches, among others, BRCAPRO and Breast and Ovarian Analysis of Disease incidence and Carrier Estimation Algorithm (BOADICEA) [20,21]. Some guidelines such as the American Cancer Society (ACS) guidelines on breast screening to identify a woman as being at high risk of breast cancer [22,23] use models based on family history which assess between 20–25% of lifetime risk for breast cancer or greater.
The Best Linear Unbiased Prediction (BLUP) Model [24] has been one of the most useful tools in animal and plant breeding with regard to the study of complex traits and nowadays this methodology is of interest to human diseases such as hereditary cancer [25]. The BLUP methodology provides an individual predicted genetic risk [26] which can be used to assess an individual’s risk of developing cancer during their lifetime which is important for genetic counseling in familial cancer, particularly in families with an unknown genetic basis. These subjects can be further studied in order to find medium-low risk alleles.
The Minnesota data breast cancer family is a historical cohort study of relatives of a consecutive series of 426 breast cancer cases, proband, identified between 1944 and 1952 [27] and have been used in familial clustering research of breast and prostate cancer [28]. The data set contains information with regard to affected status, sex, age, year of birth, father, mother, family, age at last follow up, education status, marital status, number of pregnancies and number of births.
We have used the Minnesota data breast cancer family with the aim to a) apply the BLUP methodology to estimate heritability in breast cancer in order to determine how much of the variation is due to genetic inheritance; b) propose a new individual measure for assigning a genetic additive value of cancer risk in families with a family history which is comparable with other genetic risk assessment models; c) develop an algorithm that can be used to identify individuals with a high cancer additive risk and thus aid in prioritizing families for genetic testing and/or the identification of novel genes and polymorphisms associated with cancer.
The Minnesota data breast cancer family study is available free in the R package kinship2 [29] where functions are provided to calculate a correlation matrix based on identity by descent and pedigree. The data consists of 20532 individuals of 426 families, one proband per family and a pedigree with 28082 individuals, 20532 with usable data.
1224 females presented with breast cancer.
The outcome variable is binary, assigning a value of 1 to an individual suffering cancer and a value of 0 for no cancer. When a binary trait is under study we assume an underlying continuous random variable that is normally distributed with a variance equal to one (liability). A threshold in this liability indicates when we have a case, is to say, cancer or no cancer.
From the Minnesota data, subject identifier (id), identifier of the father (fatherid), identifier of the mother (motherid), and sex were used to build a pedigree. Cancer, year of birth (yob), family identifier (family), sex, age at last follow-up (endage) and number of births (parity) were retained for the mixed model.
Year of birth, with amplitude of yob more than one century from 1842 to 1983, was used in two different ways, centered in 1920 and added as covariate in a polynomial of degree 3 or as random effect. The reason for this is to check if there could be a random environmental effect of yob (model 1) or not (model 2).
Missing values in sex, year of birth, parity and endage represent 0.07%, 23.92%, 3.36% and 32.65% of the total number of observations respectively. These values were imputed using a random forest function.
Cancer incidence per family was calculated as the number of affected individuals in the family divided by the total number of family members with cancer record available. In order to avoid the inclusion of artificial noise due to imputation, we decided not to use more explanatory variables since they have a high missing rate.
This data base was established at the 40,s last century and unfortunately there is no information regarding BRAC mutations.
Statistical analysis was performed using R [30] and packages MCMCglmm [31], kinship2 [29], missForest [32] and ROCR [33]. MCMCglmm was used to sample from mixed models equations and variance components. The kinship2 package was used for pedigree plots, and the ROCR package for ROC curves plot calculations. Finally, missForest, was used to impute continuous and categorical data allowing for non-linear relations and complex iterations.
Best Linear Unbiased Prediction (BLUP): The methodological aspects were based on BLUP trough Henderson´s mixed model equations approach [24] and Fisher´s infinitesimal model [34].
Given a linear mixed model,
\[y = X\beta + Zu + e\]
Where y is the observed phenotype, β and u is vectors of fixed and random effects, X and Z are design matrices and e is the random error.
Random effects are defined as multivariate normal distributed, MVN, u ~ MVN (0,G) and e ~ MVB (0,R) with G - genetic variance covariance matrix and R - residual variance covariance matrix.
The solution to the previous model was pointed by Henderson,
\[\left[ \begin{array}{l}
X'{R^{ - 1}}X\,\,\,X'{R^{ - 1}}Z\\
Z'{R^{ - 1}}X\,\,\,Z'{R^{ - 1}}Z + {G^{ - 1}}
\end{array} \right]\left[ \begin{array}{l}
{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}}
\over \beta } }\\
{\hat u}
\end{array} \right]\left[ \begin{array}{l}
X'{R^{ - 1}}y\\
Z'{R^{ - 1}}y
\end{array} \right]\]
In Fisher’s infinitesimal model, the genetic inheritance is based on infinite loci with a small additive effect. This genetic inheritance modified by the environment produces the observed phenotype, BLUP methodology allows us to calculate this additive part of the genetic inheritance.
The broad-sense heritability is the fraction of phenotypic variance attributable to genetic variation. When average affects, additive, of this genetic variation are taken into account, the narrow sense heritability is defined.
In this study the term heritability is defined as the additive component of the genetic variation.
Two models have been proposed and fitted which differ in the inclusion of yob as a random (model 1) or fixed effect (model 2).
In a previous variable selection step based on a generalized logistic model and according with the available information, family as a variable was discarded from the model and only sex, endage, parity and yob were retained as explanatory variables.
Model 1
Cancer ~ µ+sex+endage+parity+yob+yob2+yob3+individual
with YOB~N(0,Iσ2yob) and individual ~ (0,Aσ2individual) where I is the identity matrix, A the numerator relationship matrix whose elements are twice the coancestry between individuals [35], σ2yobthe variance given by the year of birth and σ2individual the genetic additive variance.
Model 2
Cancer ~ µ+sex+endage+parity+yob+yob2+yob3+individual
with yob as a covariate and, individual ~ N(0,Aσ2individual) where, is A the numerator relationship matrix, and σ2individual the genetic additive variance.
Both models consider that R=I, that is, there is no residual covariance between records.
Heritability estimations: Heritability was calculated to assess the additive component of the genetic variation and was calculated as follows,
\[{h^2} = \frac{{\sigma _{individual}^2}}{{\sigma _{individual}^2 + \sigma _{yob}^2 + 1}}\,\,\,{\rm{in}}\,{\rm{modle}}\,{\rm{1}}\,{\rm{and}}\,{h^2} = \frac{{\sigma _{individual}^2}}{{\sigma _{individual}^2 + 1}}\,\,\,{\rm{in}}\,{\rm{ modle }}\,{\rm{2}}\]
The consistency of our estimations for h2 was evaluated by testing the null hypothesis, H0 (h2=0/data), on the heritability using a Bayes factor against the null hypothesis calculating the marginal posterior density following the method proposed by García-Cortés et al. [36]. This method examines the posterior density of h2 =0 and calculates the probability of the alternative hypothesis (additive component) as,
\[p({H_1}/data) = \frac{1}{{1 + p({h^2}/data)}}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,(1)\]
and the probability of the null hypothesis (no additive component),
\[p({H_0}/data) = \frac{{p({h^2} = 0/data)}}{{1 + p({h^2}/data)}}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,(2)\]
Estimation of expected genetic values EGVs: Expected genetic values (EGVs) are solutions of the individual random effect, u ~ MVN(0,G ) , which are different for individuals with cancer or not. The estimation of EGV values requires the solving of the mixed model equations in Best Linear Unbiased Prediction (BLUP) section and the estimation of the variance components in Heritability estimations section. We use Bayesian inference since our outcome is dichotomous and Markov chain Monte Carlo methods have demonstrated their high performance when a binary response is the dependent variable [37]. Non parametric Kruskal Wallis test was used to assess differences in EGVs between outcome groups.
Both models, 1 and 2, were run with 151500 iterations, burning 1500 and chain was sampled every 150 iterations. Inverse Wishart with parameter expansion was assumed as prior for random effects and residual variance was fixed to one, σ2e = 1.
Converge diagnostics were assessed using Heidelberger and Welch´s test [38] in order to accept or reject the null hypothesis, the Markov chain come from a stationary distribution.
Finally in order to develop an algorithm that can be used to identify individuals with a high cancer genetic additive risk, even if we only have the pedigree and no clinical or demographic data, at the time of genetic evaluation we calculated the parental mean of EGV as a proxy of an individual EGV [39] since an individual receives half of their genetic additive inheritance from the mother and the other half from the father. Area under the Receiving Operating Curve (ROC) was used to assess the prediction ability of EGV.
For the 9 families with the largest cancer incidence rate we have also calculated the individual risk to develop breast cancer at 5 years using the Gail model [15] and the Claus model [14] using only the available information of Minnesota Breast Cancer. The variables used for the Gail model were age and number of first degree relatives affected with Breast cancer and for the Claus model; age and relationship between proband and affected relatives. These values were compared using the Pearson correlation coefficient with the corresponding EGV.
Individuals with EGV values below zero were classified as having no genetic risk of cancer whereas those with a positive value were classified as having a hereditary basis. Families with 1or 2 cancer cases were assumed as sporadic and not having a hereditary component whereas families with 3 or more cases were thought to have a hereditary component. We calculated summary statistics of EGV for these two groups of families including the mean, median and 25 and 75 percentiles and we used these values to classify the families as having a hereditary component and no hereditary component (i.e sporadic).
The outputs of Heidelberger and Welch´s test are presented in additional files (see online resources Tables ESM1 and ESM2) Model 1 and 2 reached convergence implying that our results are valid.
High posterior density intervals, HPDI provided by MCMCglmm, of variance components in Model 1 are [0.018-0.621] and [1.45-2.97] for σ2individual and σ2yob , respectively. In Model 2 HPDI for σ2individual is [0.057-0.65] which is similar to the interval obtained in Model 1.
This similarity is highlighted (see Online resources Table ESM3) where the mean and standard deviation of estimates are presented. σ2individual has a similar value in both models.
There is an additive component in cancer genetics which with regard to the Minnesota Breast Cancer data set results in heritability of 0.1 or 0.24 depending on the model specification.
HPDI for heritability is (0.017-0.174) in Model 1 and (0.058-0.396) in Model 2, in both cases HPDI did not include zero, meaning that our results are valid.
Posterior distributions for variance components in both models are presented in additional files (see online resources Figures ESM1 and ESM2). After equations 1 and 2, the test on the null hypothesis of H0 ( h2 = 0 ), results in the rejection of H0 with (H0 = 0). It can be observed that posterior density at h2 = 0 is null in both cases (Figure 1).

Figure 1: Heritability density with model 1, red, and model 2, blue.
Table 1 present’s descriptive statistics of cancer incidence, year of birth and endage for subjects of the 426 families included in the analysis, there are no significant differences in these variables between male and female subjects. Figure 2 presents cancer incidence in these families, and clearly shows that this increases steadily with the number affected cases in the family. To describe all the pedigrees is unfeasible in a paper, for this reason we present descriptive statistics of incidence, yob, number of cases, endage and sex of the 9 families with the largest and lowest incidence rate in tables 2 and 3 respectively.
|
Females |
Males |
Cancer Incidence |
0.103 |
0.016 |
End age |
65.2(16.4) |
61.7(13.6) |
Year of birth |
1924(21) |
1923(22) |
Table 1: Descriptive statistics by gender
Standard deviations in brackets
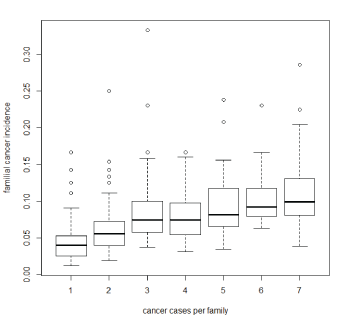
Figure 2: Cancer incidence per family, calculated as the ratio of the number of cases per family and the number of individuals, against number of cancer cases in the family.
Table 2 shows the descriptive statistics of the 9 families with the largest cancer incidence rate. Figure 3 presents pedigrees of these families, with their EGV calculated using model 1.
Family |
Incidence |
Mean yob |
Cases |
Females |
Males |
End age |
574 |
0.33 |
1932 |
3 |
6 |
5 |
48.2(12.6) |
173 |
0.28 |
1913 |
10 |
19 |
17 |
73.1(13.5) |
447 |
0.24 |
1916 |
5 |
13 |
11 |
65.1(17.4) |
289 |
0.23 |
1914 |
3 |
8 |
7 |
59.5(17.8) |
411 |
0.23 |
1933 |
6 |
14 |
20 |
56.8(11.1) |
494 |
0.22 |
1921 |
9 |
22 |
24 |
68.1(15) |
19 |
0.20 |
1911 |
5 |
12 |
12 |
70.5(11.9) |
474 |
0.20 |
1919 |
9 |
22 |
28 |
72(11.9) |
62 |
0.16 |
1926 |
4 |
15 |
16 |
61.8(20.7) |
Table 2: Descriptive statistics of the 9 families with largest cancer incidence rate
Standard deviations in brackets
Family |
Incidence |
Mean yob |
Cases |
Females |
Males |
End age |
397 |
0.019 |
1934 |
1 |
27 |
33 |
62.3(13) |
316 |
0.019 |
1926 |
2 |
73 |
73 |
68.6(13.3) |
343 |
0.018 |
1933 |
1 |
36 |
35 |
58.5(13.2) |
395 |
0.017 |
1936 |
1 |
39 |
39 |
55.5(16.8) |
453 |
0.014 |
1909 |
1 |
49 |
54 |
72.2(13.1) |
12 |
0.013 |
1926 |
1 |
46 |
51 |
66.4(16.5) |
286 |
0.0129 |
1907 |
1 |
47 |
48 |
64.9(16.1) |
433 |
0.0128 |
1930 |
1 |
53 |
54 |
61.1(14.8) |
274 |
0.0125 |
1901 |
1 |
40 |
44 |
69.5(18.2) |
353 |
0.0120 |
1913 |
1 |
48 |
46 |
68.5(16.9) |
Table 3: Descriptive statistics of the 10 families with lowest cancer incidence rate
Standard deviations in brackets
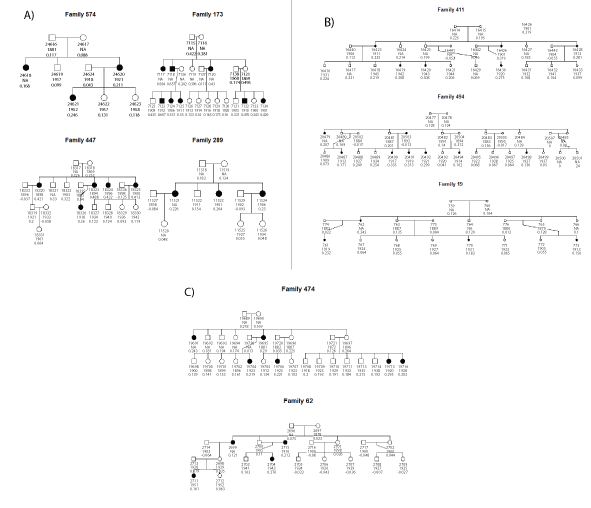
Figure 3: Families with the largest incidence rate affected in black. Numbers below symbols patient id and estimated genetic additive.
The EGV provides a measure of genetic additive risk of cancer development as exp (EGVs). Non-affected individuals are expected to have smaller and less dispersed EGVs than those affected by cancer that are larger and spread over a wider range. EGVs have interesting features. First EGVs separate non-affected versus cancer patients. Second they assess an individual genetic value for each individual, the larger the EGV the higher the probability to develop cancer and these EGVs are passed to the next generation. The genetic additive cancer risk can be calculated as the exponential of EGVs. Figure 4 shows the differences in EGVs between cancer affected and non-affected family members using model 1. A similar figure is provided as additional files for model 2 (see Online resources Figure ESM3).
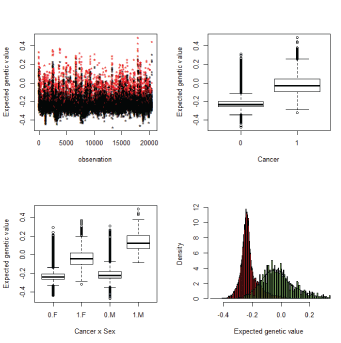
Figure 4: EGVs with Model 1. EGV are different between cancer and no cancer. Left upper panel: Red cancer, black no cancer. Right bottom panel: Distribution of EGVs for non affected, red, and cancer.
The EGV of cancer cases is higher than healthy individuals (Figure 4a) and this reached statistical significance (p<0,001) (Figure 4b). The EGV for healthy individuals were similar for males and females, whereas the EGV was higher for male cancer cases versus female cancer cases (Figure 4c).
Figure 4d shows the distribution of EGVs for affected (green) and non-affected (red) individuals. Individuals with a positive EGV have a genetic predisposition to cancer develop (marked by the dashed line) and these individuals are likely to harbor mutations or polymorphisms that increase cancer risk. EGVs were compared with cancer status to check predictive performance using ROC curves. These ROC curves and 95 % confidence intervals of area under the ROC curve (AUC) were drawn (see online resources Figure ESM4). Model 1 and 2 show similar large AUC values, 0.93-0.94, therefore when an individual has a high positive EGV this indicates a high genetic predisposition to cancer in comparison with those which have a large negative EGV
These features explain how EGVs and the observed phenotype are linked and on the other hand the biological meaning of EGVs.
Since an EGV of an individual is ½ of the father’s EGV plus ½ of the mother´s EGV, we predicted the cancer status using this parental mean and we used t this value as a proxy of individual EGV (Figure 5a). The prediction ability of these mean values tested with the corresponding AUC, with a good AUC performance of 0.713-0.791 (Figure 5b).
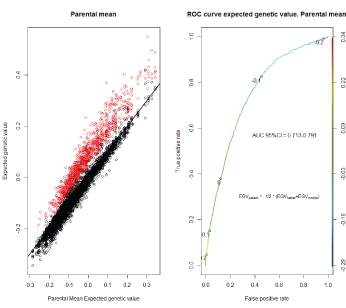
Figure 5: Parents mean Expected genetic value versus offspring Expected genetic value. In red, cancer, left panel. ROC curve using parental mean EGV, right panel, Model 2.
Figure 6 provides a comparison between the BLUP genetic risk estimation and the Gail model where risk values are plotted and there was a statistically significant correlation of 0.6 [0.44-0.73] p<0.01 between the two values. In addition, correlation between BLUP genetic risk estimation and cumulative probability of Breast cancer under the Claus model [14] gives a significant correlation of 0.23 [0.02-0.42].
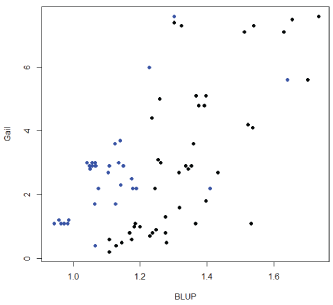
Figure 6: Comparison between BLUP genetic risk estimation, EGV, and Gail model for the 10 families with large cancer incidence. Black dots indicates affected. Blue dots non affected.
In figure 7 we show the number of individuals in a family with a positive EGV (i.e. a genetic predisposition to cancer). We can distinguish between families with several members with a positive EGV that are likely to harbor medium-high risk alleles (right hand side of dashed line) from those that have a few members with positive EGV and thus are likely to harbor low-medium risk alleles with a variable penetrance (left hand side of dashed line).
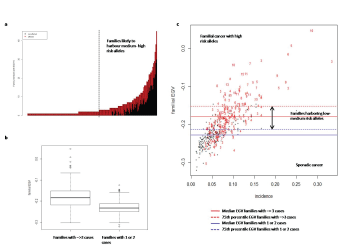
Figure 7: Using EGV values to classify the families as sporadic or with a hereditary component. a. Frequency of individuals in a family with a positive EGV value. b. median EGV of families with 1 or 2 cases in the family (sporadic) or 3 or more cases (hereditary). c. Plot of median family EGV value with cancer incidence (i.e. genetic risk).
The median EGV for families with 1 or 2 cancer cases (which would normally be considered as sporadic) was -0.23 (-0.25, -0.21, 25 and 75 percentiles respectively), whereas the median EGV of families with 3 or more cases (which depending on the relationship of affected individual’s would be considered as having a hereditary component) was-0.18 (-0.21, -0.15, 25 and 75 percentiles respectively) (Figure 7b) The median EGV is significantly higher in families with 3 or more cases (-0.18) than families with 1 or 2 cases (p<0.001). As demonstrated in figure 7c we have used these values as criteria to classify and define families as sporadic or with a hereditary component. We have classified those families with an EGV below the median value of families with 1-2 cases as sporadic cancer families. The families with a hereditary component are defined as those with an EGV above the 75th percentile of the EGV of families with only 1 or 2 cases. We further define the families with a hereditary component into those that are likely to harbor high risk alleles such as BRCA2 mutations, i.e. those with an EGV greater than the 75th percentile of the EGV of families with 3 or more cases. As well as families that are likely to harbor low-medium risk alleles, i.e. those with an EGV between the 75th percentile of families with 1 or 2 cases and the 75th percentile of families with 3 or more cases. It is of note that there are families with 3-5 cases of cancer that have median EGV in the sporadic cancer range. The clustering of cancer in these families does not appear to have a hereditary component and may be due to a shared environmental risk factor. Thus genetic testing in these families would be inappropriate and this model provides a tool to assess the hereditary component in these families before deciding on genetic testing.
The BLUP model heritability value applied in this study of families with breast cancer differs from zero and highlights the validity of the polygenic inheritance pattern. EGV are able to discriminate between cancer and no cancer subjects and provides a tool for hereditary cancer counseling since they provide an individual risk assessment even if the patient has not yet develop cancer. Given the binary nature of the outcome, the results presented in this paper are reliable and accurate.
EGV can be estimated more precisely by adding clinical, pathological and socio-demographic data; however these data are not usually available. Data with regard to the presence of germline mutations in susceptibility genes can be easily incorporated at a later stage into the model as it becomes available. Indeed, genomic information could be used in combination with the pedigree or alone to calculate a more accurate relationship matrix [40]. Moreover, even if a family tree cannot be constructed due to lack of information, the genomic era and the derived genetic data allows us to construct a more accurate relationship matrix than that derived from the pedigree. In fact the high quantity and quality genetic data generated from next generation sequencing technologies facilitate identity by descent (IBD) calculations and also us to compare long stretches of consecutive homozygous genotypes, so called runs of homozygosity, ROHs [41] identifying relationships between individuals not considered in pedigree based methods [35].
The bimodal distribution of EGV in breast cancer obtained here are similar to those calculated by Vazquez et al. [26] in skin cancer using BLUP based on pedigree or genomic information. Although these authors found better cancer prediction ability in terms of ROC area for the genomic information model than the pedigree model, 0.58 vs 0.63, the improvement in percentage terms was 8% and the genomic information was not used to construct a relationship matrix. On the other hand the economical expenses of a pedigree based method are lower than those which need genomic information.
The polygenic inheritance approach of BLUP provides a more realistic model of familial breast cancer in the absence of a known germline mutation than those that assume a single major allelic locus [14].
BLUP methodology is also used with shrinkage methods such Riddge, Lasso and Elastic Net [42,43] in order to reduce the high dimensionality of the data and to select significant variables. In fact BLUP works as a shrinkage method giving more importance to the genetic part of the model when heritability is high and penalizing the non-genetic terms of the model.
In the clinical practice an evaluating scheme of hereditary cancer can be established by setting-up a data base with all the pedigrees and clinical variables in order to calculate BLUP estimates for each individual and providing a reference measure when new affected families that need genetic counseling join the scheme. Even though male breast cancer does not appear to have a genetic component, they are evaluated and their genetic additive value is transmitted to the next generation. This is a relevant feature of BLUP, since other risk models assign the same value to a group of siblings [44].
Figure 3, illustrates this procedure where BLUP estimates within the same family discriminate risk between relatives which share the same number of affected relatives. As an example, in families 173,494, and 474, the third generation of cousins differs with regard to their genetic additive value. In family 173 in the 3rd generation there are three groups of cousins. The parents of two of them are affected. Descendants of 7118 and 7136 have the larger EGV (higher genetic risk), followed by the descendants of 7138 and 7121, and finally the descendants of 7137 and 7120 have the smallest expected genetic value but still have a genetic risk.
Figure 5 shows that as quantitative genetics highlighted, it is possible to calculate a value for offspring defined as the average value of the parents plus a random Mendelian noise factor, [39] which can be used in genetic counseling as an approximate prediction of EGV, giving a value to the clinician about the genetic cancer risk of the future offspring.
There is still a lot of speculation with regard to the management of families without a pathogenic germline mutation or carriers of variants of unknown significance in susceptibility genes, especially with regard to the age to start screening, the screening modality (mammography or MRI) and the recommendation of prophylactic surgery or preventative chemotherapy. These types of model could be most useful in these types of families for which the guidelines are not as clear. This information can help to prioritize individuals for screening and family members with a larger genetic additive values should be screened accordingly, in order to identify a cancer at a potentially curable stage.
The Gail model is used in the clinic to determine the probability of developing cancer within the next five years, whereas the BLUP method estimates lifetime genetic risk. We compared the risk assessment value of the Gail model with our model and a positive correlation was found between both models, indicating that they share the same underlying mechanism of cancer risk development but the risk values are interpreted differently. Gail model uses a given number of relatives in their estimation but BLUP is able to use the entire familial tree.
The Claus model assumes a single diallelic major locus as the underlying cause of susceptibility to breast cancer, whereas the BLUP model proposes a polygenic additive model and this is the reason why correlation between both models were low.
There are also other models to predict genetic cancer risk such as the BOADICEA model [45] which estimates based on age, whereas BLUP calculates genetics risk independently of age, sex or other confounders. Secondly, BOADICEA calculates a risk individual by individual, whereas BLUP evaluates all individuals at once given the possibility to have the EGVs of an entire population in a single step and saving time in the genetic counseling.
The BLUP method provides a novel application to the hereditary cancer setting that other models in use in cancer genetics do not offer. As presented in figure 7, BLUP can identify families with a large EGV, i.e. families with hereditary cancer and can help distinguish between those families that are likely to harbor high risk alleles (such as BRCA mutations) and families with low-medium risk alleles. The BLUP method can help us to identify families candidates to explore their genetic background looking for rarer polymorphisms via high density next generation sequencing. As well as deciphering the impact on risk of the many variants of unknown significance identified in BRCA1 and BRCA2 genes and others.
BLUP model can be applied to other breast cancer populations or other cancer types in order to validate these results. This model also provides a reliable estimation of genetic cancer risk independently of environmental factors in a single step, assuming a polygenic underlying mechanism for cancer susceptibility, in contrast to the Gail and Claus models.
The results obtained give a reliable estimation of heritability different from zero in breast cancer and provide meaningful genetic additive values for each individual.
We have obtained a reliable estimation of heritability for breast cancer between 0.1- 0.2, different from zero, and meaningful additive values of cancer in Minnesota Breast data set for each individual. These values alone or in combination with other methods improve cancer prediction in the hereditary cancer setting as well as the identification of novel genes/ polymorphisms related with cancer and the assessment of the impact of variations on unknown significance on breast cancer risk. BLUP is able to incorporate clinical and pathological information in the estimations and consider a polygenic inheritance model instead of an autosomal dominant model.
BLUP provides an additional tool for use in hereditary cancer and estimates the extent of heritability of cancer, calculating an individual genetic risk of cancer in family members and an approximation of the genetic risk of future descendants. In addition this tool can be used to assess the genetic basis of hereditary cancer in these families, either due to high risk alleles for low-medium risk alleles.
JCMA and LAGC designed the study and developed the statistical analysis tools and wrote the manuscript.
JCMA contributed to the statistical programming in R and LAGC test the posterior density of heritability.
JE and CGP provided expertise in clinical cancer for the application of the BLUP methodology to clinical cancer research and also wrote the manuscript.
All authors reviewed, commented and approved the manuscript.
The authors thank Marta Rava for her valuable comments in the manuscript.
Author JC Martínez Avila, Author C Guillen-Ponce, Author J Earl and Author LA García-Cortés declare that they have no conflict of interest.
Data used in this work is free available at the R package kinship2. Data corresponds to Minnesota data breast cancer family study. Subjects in this data set are anonymized.
Download Provisional PDF Here
Article Type: Research Article
Citation: Martínez-Ávila JC, Guillén-Ponce C, Earl J, García-Cortés LA (2016) Hereditary Lifetime Cancer Risk Assessment Modeling: A Case Study in Breast Cancer. Int J Mol Genet and Gene Ther 2(1): doi http://dx.doi.org/10.16966/2471-4968.106
Copyright: © 2016 Martínez-Ávila JC, et al. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Publication history:
All Sci Forschen Journals are Open Access